Week 8: Geostatistics–Kriging

1 Introduction

• In this Lab, we will learn two key functions
  • krige.control: specify the parameter for kriging, no computing involved.
  • krige.conv: to compute

• Usage
  • krige.control(type.krige = “ok”, obj.model = NULL)
  • Type of krige: “sk”, “ok” (default)
  • obj.model: typically an output of likefit

• Usage
  • krige.conv(geodata, locations, krige)
  • geodata
  • locations: \(\mathbf s_0\), data.frame, multiple locations.
  • krige: output of krige.control.

2 Ordinary Kriging

First, we fit the model \[Z(\mathbf{s}) = \mu + U(\mathbf{s}) + \nu(\mathbf{s}).\] Here trend = “cte” specifies that the trend \(\mu(\mathbf{s})\) is a constant (\(\mu(\mathbf{s})=\mu\)).

library(geoR)
data(ca20)
fit = likfit(ca20, ini = c(100, 120), trend = "cte")

Secod, we setup the Ordinary Kriging.

pred_locs = expand.grid(x = seq(5300, 5800, 10), y = seq(5000,5600, 10))   # new locations s_0 created
head(pred_locs)     ## Here are the first six locations

##      x    y
## 1 5300 5000
## 2 5310 5000
## 3 5320 5000
## 4 5330 5000
## 5 5340 5000
## 6 5350 5000

KC = krige.control(obj.model = fit)

Third, we make predictions on all locations on gr

ca20pred = krige.conv(ca20, loc = pred_locs, krige = KC)

• The output includes
  • ca20pred$predict: the kriging estimates for all locations specified at loc.
  • ca20pred$krige.var: the kriging variance for all locations specified at loc.

Last, we visualise both Kriging estimates and Kriging variances. The function to use is geom_tile

ca20_res = data.frame(x = pred_locs[,1], y = pred_locs[,2], 
                      krige = ca20pred$predict, krige_var = ca20pred$krige.var)


library(ggplot2)
ggplot(ca20_res) + geom_tile(aes(x = x, y = y, fill = krige))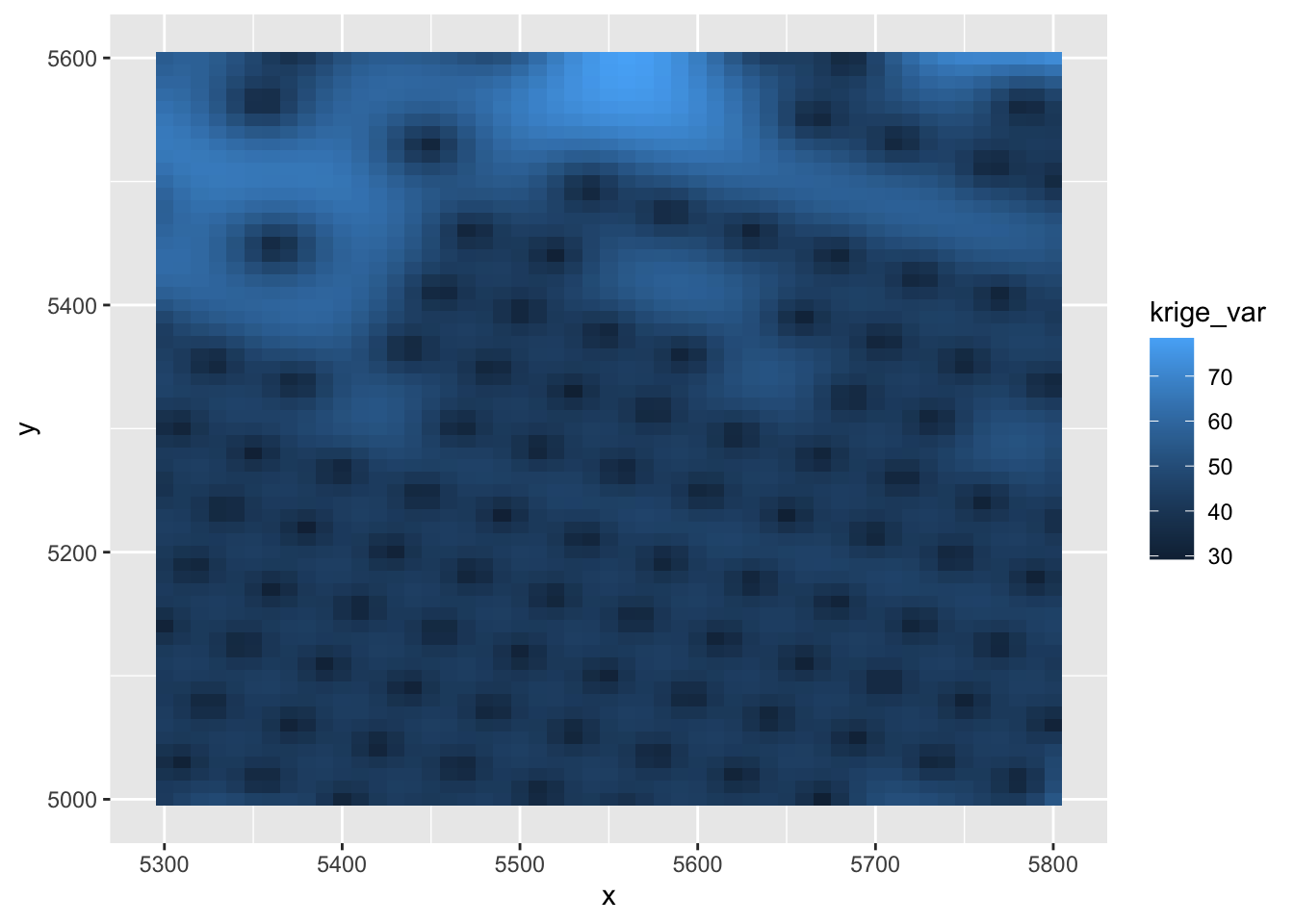

Kriging Variances

ggplot(ca20_res) + geom_tile(aes(x = x, y = y, fill = krige_var))

Kriging weights

coords = cbind(c(0.2, 0.25, 0.6, 0.7), 
               c(0.1, 0.8, 0.9, 0.3))   # data
KC = krige.control(ty = "ok", cov.model = "mat", 
                   kap = 1.5, nug = 0.1, 
                   cov.pars = c(1, 0.1))    # model parameter
# Weights
krweights(coords, c(0.5, 0.5), KC)                              

## [1] 0.1935404 0.2301559 0.2125838 0.3637199

3 Universal Kriging

Both ordinary kriging and universal kriging using setting type.krige = “ok”. Once you put the trend in, the function will distinguish two types of kriging.

3.1 Universal Kriging: Polynomial of coordinates

• We need to provide \(x_1(\mathbf s_0), \ldots, x_p(\mathbf s_0)\) for the function
  • in function krige.control
  • trend.d: specify data trend
  • trend.l: specify prediction trend

Work with polynomial.

fit = likfit(ca20, ini = c(100, 60), trend = "1st")
gr = pred_grid(ca20$borders, by = 10)
KC = krige.control(obj.model = fit, trend.l="1st", 
                   trend.d="1st")
ca20pred = krige.conv(ca20, loc = gr, krige = KC)

3.2 Universal Kriging: covariates

fit2 = likfit(ca20, ini = c(100, 60), trend = ~altitude)
gr = pred_grid(ca20$borders, by = 10)
graltitude = rnorm(10908,mean=5.5)
KC2 = krige.control(type.krige = "ok", obj.model=fit2, 
                    trend.d=~altitude, trend.l=~graltitude)
ca20pred2 = krige.conv(ca20, loc = gr, krige = KC2)

In universal kriging, we need to know \(x(\mathbf s_0)\). In the above code, I randomly generated \(x(\mathbf s_0)\) from graltitude = rnorm(10908,mean=5.5). In practice, you shall know \(x(\mathbf s_0)\) in advance.