1 Dataset

library(ggplot2)
library(sf)
library(maps)
library(dplyr)
library(spData)
library(spdep)
library(spatialreg)

We want to study the relationship between price of used cars and the taxes charged across 48 states in 1960
- tax.charges: taxes and delivery charges for 1955-9 new cars
- price.1960: 1960 used car prices by state

data(used.cars)
head(used.cars)

##    tax.charges price.1960
## AL         129       1461
## AZ         218       1601
## AR         176       1469
## CA         252       1611
## CO         186       1606
## CT         154       1491

2 Visualisation

First, we read into the us states maps and convert it the sf object.

state_sf = sf::st_as_sf(maps::map("state", plot = FALSE, fill = TRUE))

Note that the state names in used_cars are abbreviation while full names in state_sf. We want to combine these datasets together by names, and used state.csv which includes both abbreviation and full names of all states.

abb = read.csv("datasets/states.csv")
abb = abb |> mutate(state_lower = tolower(State))
used.cars$Abbreviation = rownames(used.cars)

head(abb)

##        State Abbreviation state_lower
## 1    Alabama           AL     alabama
## 2     Alaska           AK      alaska
## 3    Arizona           AZ     arizona
## 4   Arkansas           AR    arkansas
## 5 California           CA  california
## 6   Colorado           CO    colorado

head(state_sf)

## Simple feature collection with 6 features and 1 field
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -124.3834 ymin: 30.24071 xmax: -71.78015 ymax: 42.04937
## Geodetic CRS:  +proj=longlat +ellps=clrk66 +no_defs +type=crs
##                      ID                           geom
## alabama         alabama MULTIPOLYGON (((-87.46201 3...
## arizona         arizona MULTIPOLYGON (((-114.6374 3...
## arkansas       arkansas MULTIPOLYGON (((-94.05103 3...
## california   california MULTIPOLYGON (((-120.006 42...
## colorado       colorado MULTIPOLYGON (((-102.0552 4...
## connecticut connecticut MULTIPOLYGON (((-73.49902 4...

used = state_sf |> rename(state_lower = ID) |> left_join(abb, by = "state_lower") |> right_join(used.cars, by = "Abbreviation") |> rename(price = price.1960, tax = tax.charges)

Next, we visualise the price variable and tax variable. We can see there is a spatial dependence for both variables.

ggplot() + geom_sf(data = used, aes(fill = price))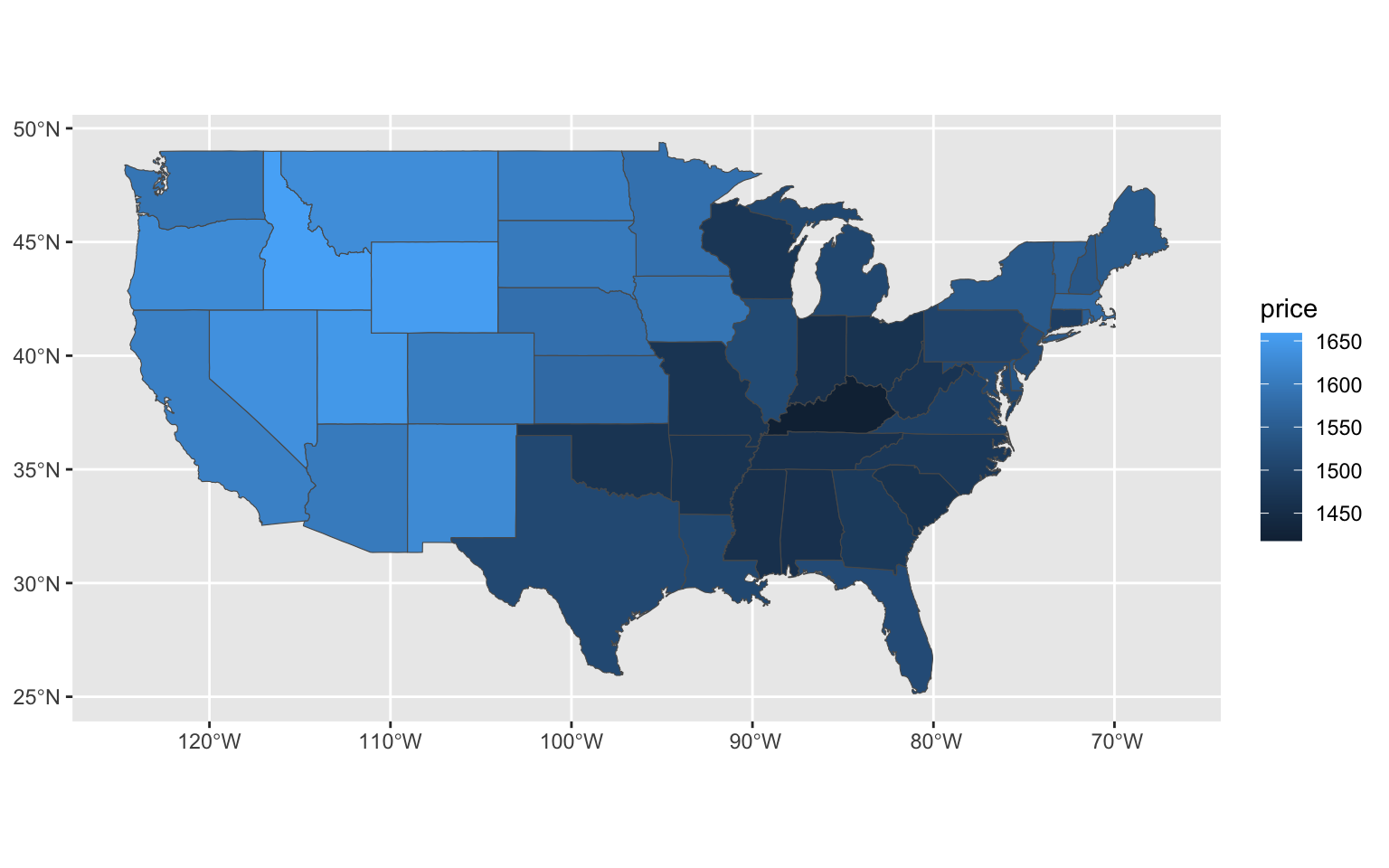

ggplot() + geom_sf(data = used, aes(fill = tax))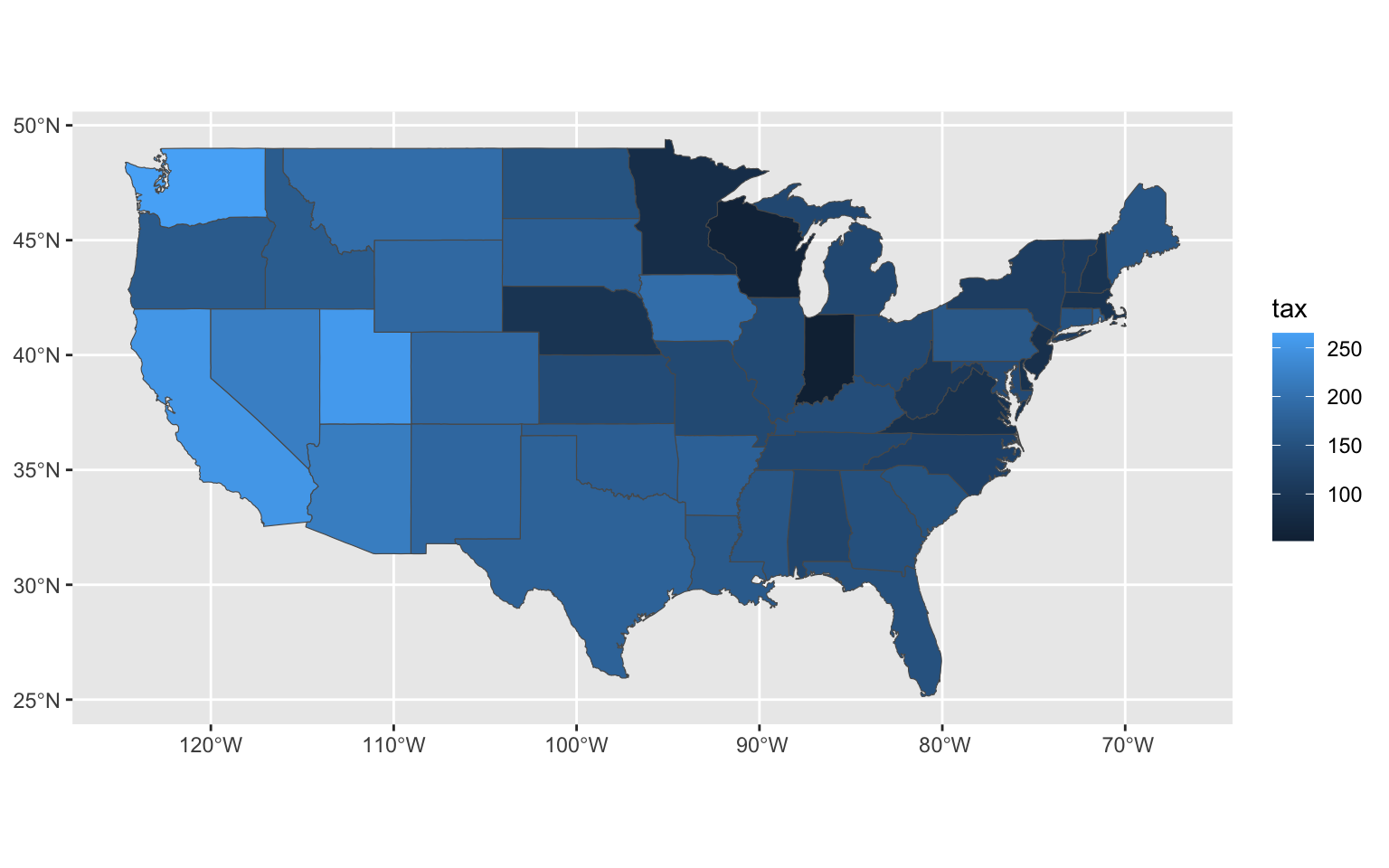

2.1 Spatial Dependence

moran.test(used$price, nb2listw(usa48.nb))

## 
##  Moran I test under randomisation
## 
## data:  used$price  
## weights: nb2listw(usa48.nb)    
## 
## Moran I statistic standard deviate = 8.1752, p-value < 2.2e-16
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic       Expectation          Variance 
##       0.783561543      -0.021276596       0.009692214

moran.plot(used$price, nb2listw(usa48.nb),
           labels=used$Abbreviation)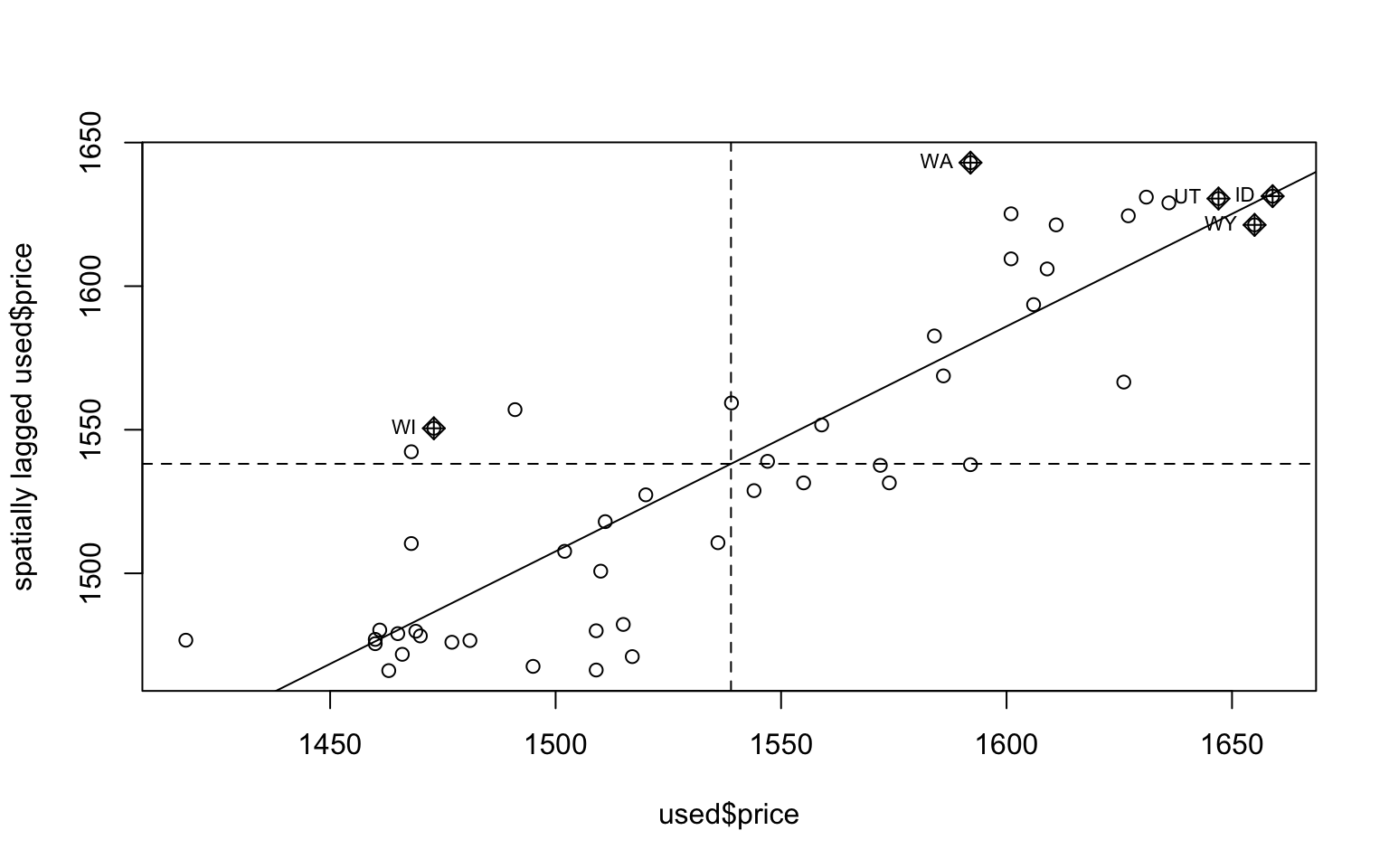

3 Modelling

3.1 OLS

If we fit a linear model, we can see the resulting residuals are still spatially correlaed.

mod_ls <- lm(price ~ tax, data=used)
summary(mod_ls)

## 
## Call:
## lm(formula = price ~ tax, data = used)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -116.701  -45.053   -1.461   43.400  107.807 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1435.7506    27.5796  52.058  < 2e-16 ***
## tax            0.6872     0.1754   3.918 0.000294 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 57.01 on 46 degrees of freedom
## Multiple R-squared:  0.2503, Adjusted R-squared:  0.234 
## F-statistic: 15.35 on 1 and 46 DF,  p-value: 0.0002939

used$res = mod_ls$residuals
ggplot() + geom_sf(data = used, aes(fill = res))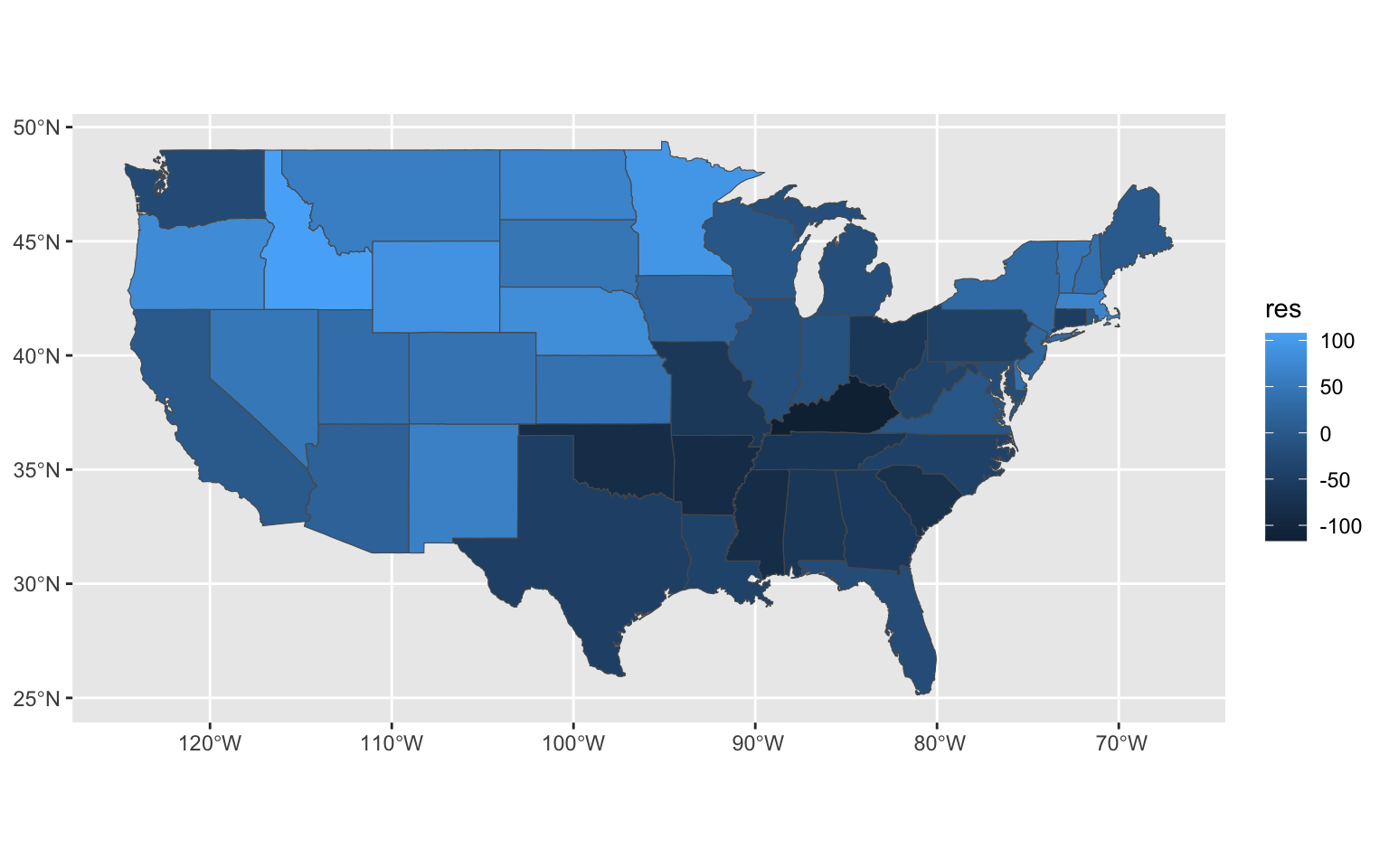

3.2 Spatial Lag Model

mod_lag <- lagsarlm(price ~ tax, data=used,
                   nb2listw(usa48.nb))
summary(mod_lag)

## 
## Call:lagsarlm(formula = price ~ tax, data = used, listw = nb2listw(usa48.nb))
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -77.6781 -16.9504   4.2497  19.5484  58.9811 
## 
## Type: lag 
## Coefficients: (asymptotic standard errors) 
##              Estimate Std. Error z value Pr(>|z|)
## (Intercept) 309.42546  123.03167  2.5150   0.0119
## tax           0.16711    0.10212  1.6364   0.1018
## 
## Rho: 0.78302, LR test value: 42.681, p-value: 6.4426e-11
## Asymptotic standard error: 0.081636
##     z-value: 9.5916, p-value: < 2.22e-16
## Wald statistic: 91.998, p-value: < 2.22e-16
## 
## Log likelihood: -239.8252 for lag model
## ML residual variance (sigma squared): 1036.7, (sigma: 32.197)
## Number of observations: 48 
## Number of parameters estimated: 4 
## AIC: 487.65, (AIC for lm: 528.33)
## LM test for residual autocorrelation
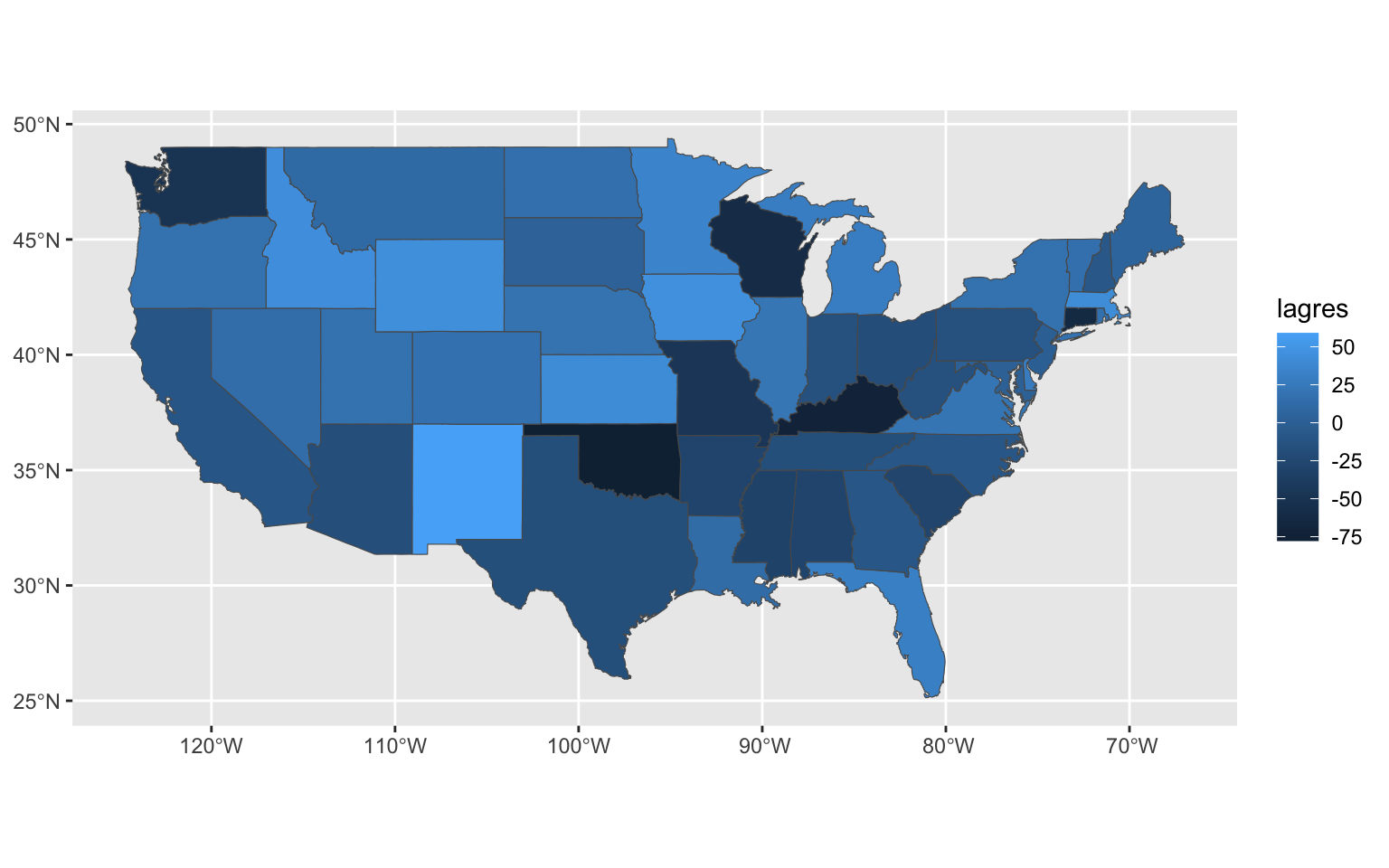
## test value: 2.1141, p-value: 0.14594

used$lagres = mod_lag$residuals
ggplot() + geom_sf(data = used, aes(fill = lagres))